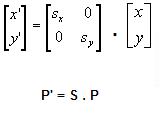A Scaling transformation alters the size of an object.Scaling is carried out by applying scaling factors sx,sy for x and y direction.
The transformation equations to scale the point P(x,y) with scaling factors sx and sy is given by
x'= x . sx,y'= y . sy
where sx scales the object in the x direction and sy scales in the y direction
sx and sy can be assigned any positive number.Values less than 1 reduce the size of the object.Values greater than 1 increase the size of the object.
sx=sy = 1 leaves the object and changed
If sx and sy are given same value, uniform scaling is produced
unequal values for sx and sy produced differential scaling. Object are both scaled and repositioned.Scaling factors with values less than 1 move the objects closer to origin and values greater than 1 move the objects away from the origin.

In matrix form,